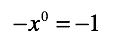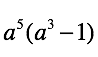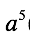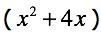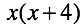Evaluating Expressions
If you need to evaluate an expression,
just replace the variable
(the letter) with the number given.
Here are some examples:
1) Evaluate: 3A + 3B
if A=2 and B=6
Plug the value 2 for every letter A and
the value 6 for the letter B
3(2) +3(6) =
6 + 18=
24
2) Evaluate: 2y-5t-7v
if y=1, t=6, v=-1
Plug the value 1 for every letter y, the value 6 for the letter t,
and -1 for the letter v.
2(1)-5(6)-7(-1)=
2-30+7=
-21
Let's Practice
Let's Practice
Let's Practice
Let's Practice
Let's Practice
When simplifying expressions,
you need to group all the like terms together.
For example:
Simplify the following expression:
3X+ 2Y-4X+6Y
Group together the terms that are alike:
3X-4X + 2Y+6Y= -X+ 8Y
Let’s do another example:
2(x-2y)-(x+3y)
Let’s do the parenthesis first, by distributing the 2 and the negative (-)
in front of the parenthesis
2x-4y-x-3y
Now, just group the like terms:
2x-x-4y-3y
2x-7y
Another example:
-3a(4+b)-4b(3-a)
Let’s distribute the numbers in front of the parenthesis:
-12a-3ab-12b+4ab
Now you can group the like terms:
-12a-12b+ab
Expressions can be translated from English to a math expression
or vice versa.
There are key words to use when you are translating an expression.
Let’s learn the rules to treat exponents with examples:
Rule 1:
When you multiply exponents with the same base, you need to keep the base and add the exponents on the top:
Examples
Rule 2:
When you have a negative exponent, you can change it
to positive by finding its inverse:
Examples
Rule 3:
When you are raising a power to a power, you need to multiply:
Examples
Rule 4:
When you divide exponents with the same base, you will subtract them
Examples
Rule 5:
When you raise an exponent to ZERO, the answer is 1.
**Be Careful, if you have a negative in front,
then the answer is -1.
BUT, if you have it with a parenthesis like this, then the answer is 1
When you multiply polynomials, you need to follow
the rules of exponents.
Let’s do an example:
Distribute the variables xy to every single term:
Let’s do another example:
Simplify
(3x-y)(x+2y)
STEP ONE: Multiply the 3x by every single term on the second parenthesis
and the same with -y
STEP TWO: Just group the terms
Another example:
(a-b)(a+b)
Let’s do an example:
Factor the following expression by the GCF
The Greatest Common Factor is
the letter with the lowest exponent then you can factor out and you have :
Let’s do another example:
The GCF is 2xy, that is the most you can extract from the binomial
2xy(2x-1)
When you factor by grouping you will have four terms
Let's do an example:
The first step is to make an invisible line between
the four factors and find the GCF for and (5x+20)
The GFC for is X
The GCF for 5x+20 is 4
5x+20=5(x+4)
Now we can factor the X for the first term:
Finally
(X+5)(X+4)